有1000瓶水,其中有一瓶有毒,小白鼠只要尝一点带毒的水24小时后就会死亡,至少要多少只小白鼠才能在24小时时鉴别出哪瓶水有毒?
这是一道很经典的面试题目,先说解题方法吧,2^n >= 1000,其中n就是小白鼠的数量。如果知道答案了,也许很多人就恍然大雾,当然有些专业的人士用下面的归纳法证明了下:
-
当n=1时,即有2瓶水,任取一瓶水喂老鼠,若24小时后老鼠死,则此瓶水有毒;若24小时后老鼠没死,则此瓶水无毒,另一瓶水有毒。课件只需一个老鼠即可判断出哪瓶有毒。即当n=1时命题成立。
-
假设当n=k(k>1)时,命题为真。即须k只老鼠即可判断出哪瓶水有毒。 则当n=k+1时,即有2^(n+1)瓶水。 将水分成2组,命名为P1和P2,每组2^n瓶水. 则这两组瓶中有一组全没毒,另一组中有仅一瓶有毒。 a) 取1只老鼠、任取一组瓶子,假设为P1,将P1中的全部瓶子水都让老鼠尝一下。则24小时后可以根据此老鼠的生死情况判断毒药在哪一组。 b) 取k只老鼠,根据假设可知当n=k时,可判断哪瓶水有毒。用这k只老鼠同时去检测P1和P2,则24小时后可挑出P1中的某一瓶和P2中的某一瓶,这两瓶可能有毒。 根据a、b中的结果综合分析,可得知毒药瓶是哪一个。 即当n=k+1时,命题为真。
命题得证。
这个证明应该是没问题,但是我很感兴趣的就是,如何猜出来这个命题的哪?我就说下这个过程吧,来检测瓶中的水有没有毒,只能靠小白鼠死没死亡来判断,也就是2种状态,这里1表示死亡,0表示存活。那么10个小白鼠,那么可以表示2^10(代表10次方)中状态,也就是1024。那么这1024种状态能不能对应出那瓶水有毒那,如果可以这个题目就解决了。看到这里,又回到了上面的证明,这个归纳法明显可以证明,此猜想没问题。由此归纳法可以看出,此问题符合算法中的,动态规划法,也就是该问题可以分解成更小的问题,1000(也就是1024瓶以内)瓶水给10个老鼠喝,512(512瓶水以内)瓶水给9个老鼠喝…以此类推,平且每个大问题的子问题,还跟这个大问题有关系,由数学归纳法证明的第二步,可以看出,通过子问题的解决,更大的问题带入到步骤2中就可以解决了。
以上步骤说了半天都是,说明此方法是正确的,可证明的。但是如果要问怎么安排老鼠喝水,才能判断那瓶有毒那?也就是把这个动态规划的算法如何来实现。其实改归纳法证明中的第二步骤中的b)后面的内容,已经透露出了运用的实现方法。也就是把有所有的水给某一个老鼠P10喝,剩下的老鼠喝的水都不能包含P10喝的那瓶毒水,那么如果P10死亡了,剩下的都活着,就检查出来毒水了。以此类推老鼠P9喝的水肯定包含一瓶其他老鼠都没喝过的,这样才能检查出这瓶水有毒。这样我们就可以得出下面的结论:
1 表示死亡 0 表示存活
0000000001 P1喝了第一瓶的水,其他老鼠都没喝,那么P1老鼠死亡,其他没死推断出第1瓶水有毒
0000000010 P2喝了第二瓶的水,其他老鼠都没喝,那么P2老鼠死亡,其他没死推断出第2瓶水有毒
0000000100 P3喝了第4(2^2)瓶的水,其他老鼠都没喝,那么P3老鼠死亡,其他没死推断出第4(2^2)瓶水有毒
……
这里开始有疑问了,那么从第2—第4瓶水,中间的那瓶水有毒如何推断那?这里就用到一个方法叫组合。11代表第3瓶水有毒,也就是P1和P2必须同时喝第三瓶水,而P3不能喝,那么P1和P2死,P3没死就可以得出第三瓶水有毒。下面的各瓶水的判断,都快可以依据这个理论类推,根据上面数学归纳的证明,应该可以判断出来所有的剩余的水。这里可以发现一个显而易见的规律,P1老鼠所有奇数位置的水都得喝,因为P1老鼠可以测试有毒瓶子的位置为xxxxxxxxx1 (x代表未知),换成10进制必须包含一个2^0也就是1,那显然是奇数。只有这样才能组合出水的位置,从刚才第三瓶水的判断也可以看出。P2老鼠喝水当然也有规律了,xxxxxxxx1x,换成10进制必须包含2^1也就是2,根据2进制转换成10进制的算法,我们看下面的数字4=2^2 , 3=2^1 + 2 ^ 1 , 2 = 2^1 , 1=2^0其中3就包含了2^1方,也就是3号瓶子的水,P2必须喝,根据这个方法5=2^2 + 2^0那么5号p2就不用喝,我们总结下就可以看出,其实P2如果换成10进制的话,每隔2个位置就需要P2喝,也就是6,8,10,12…都需要。那么P3那同理根据这个推算方式,每隔4个位置就需要P3喝,也就是4,8,12…。至此所有的老鼠应该喝的水所在的瓶子的位置都判断出来了。
上面的方法,讲完后,如果你学习过计算机网络中海明码的编码规则,那你岂不是就恍然大悟了。这不就是海明码的编码规则么?下面我们就对比下海明码的编码规则:







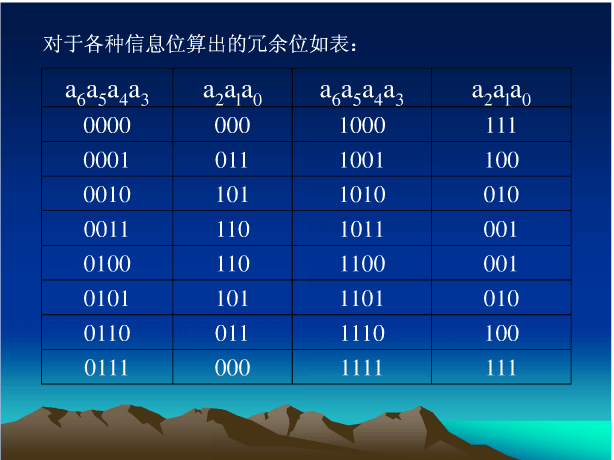
下面看如何计算海明码(Hamming Code )
海明码(Hamming Code )编码的关键是使用多余的奇偶校验位来识别一位错误。
码字(Code Word) 按如下方法构建:
-
把所有2的幂次方的数据位标记为奇偶校验位(编号为1, 2, 4, 8, 16, 32, 64等的位置)
-
其他数据位用于待编码数据. (编号为3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17等的位置)
-
每个奇偶校验位的值代表了代码字中部分数据位的奇偶性,其所在位置决定了要校验和跳过的比特位顺序。
位置1:校验1位,跳过1位,校验1位,跳过1位(1,3,5,7,9,11,13,15,…) 这里和老鼠和水的位置是不是一样的
位置2:校验2位,跳过2位,校验2位,跳过2位 (2,3,6,7,10,11,14,15,…)
位置4:校验4位,跳过4位,校验4位,跳过4位(4,5,6,7,12,13,14,15,20,21,22,23,…)
位置8:校验8位,跳过8位,校验8位,跳过8位(8-15,24-31,40-47,…)
…
如果全部校验的位置中有奇数个1,把该奇偶校验位置为1;如果全部校验的位置中有偶数个1,把该奇偶校验位置为0.
举例说明:
一个字节的数据:10011010
构造数据字(Data Word),对应的校验位留空_ _ 1 _ 0 0 1 _ 1 0 1 0
计算每个校验位的奇偶性 ( ?代表要设置的比特位):
位置1检查1,3,5,7,9,11:
? 1 0 0 1 _ 1 0 1 0. 偶数个1,因此位置1设为0,即: 0 _ 1 _ 0 0 1 _ 1 0 1 0
位置2检查2,3,6,7,10,11:
0 ? 1 _ 0 0 1 _ 1 0 1 0. 奇数个1,因此位置2设为1,即: 0 1 1 _ 0 0 1 _ 1 0 1 0
位置4检查4,5,6,7,12:
0 1 1 ? 0 0 1 _ 1 0 1 0. 奇数个1,因此位置4设为1,即: 0 1 1 1 0 0 1 _ 1 0 1 0
位置8检查8,9,10,11,12:
0 1 1 1 0 0 1 ? 1 0 1 0. 偶数个1,因此位置8设为0,即: 0 1 1 1 0 0 1 0 1 0 1 0
因此码字为: 011100101010.
查找并纠错一位错误
上例中构建了一个码字 011100101010,假定实际接收到的数据是011100101110. 则接收方可以计算出哪一位出错并对其进行更正。方法就是验证每一个校验位。记下所有出错的校验位,可以发现校验位2和8的数据不正确. 错误校验位 2 + 8 = 10, 则位置10的数据出错。一般说来,对所有校验位进行检查, 将所有出错的校验位置相加, 得到的就是错误信息所在的位置.
至此终于发现原来这个面试题目,使我们学过的。是不是感觉自己学的东西太糙了么? 原文链接
