最近刚做完一个项目,闲了下来。想分享下关于软件复杂度的一些思考。这里先说下文章标题的由来,一个软件产品对于用户来讲,好看好用是必须的,其次就是看这个软件的性能好不好,不要老是卡和崩溃。如果满足这两点,往往这个软件口碑不会差。所以对于开发人员来讲,写代码时一定要关注产品的体验和性能。
对于一个软件产品就跟一个人一样。这个人长的好不好看、脑子聪不聪明确实很重要。所以很多时候我们看一个人,往往比较关注他的外表和智力。那么对比于软件开发,程序员们也是很重视代码的实现和性能,所以你可以看到大量讨论实现和算法的文章。可是这里所说的“德”就往往很容易被忽略。
那何为“德”,说的直接一点就是约束自己,方便别人。为什么要做这种吃力不讨好的事情呢?是因为道德放在一个长线来看,是对大家都有好处的,否则大家只做利己的行为这个社会可能会乱成一锅粥。那么对于写代码要讲武德,也就是我们在实现一个功能时,尽量让后面接手的人容易看懂,而不要仅仅是实现了功能和用了牛逼的算法优化了性能,也关注下这个“德”,就跟人一样要德智体全面发展。对于写代码来说这个“德”如何做呢?下面我们就来看软件复杂度的管理。
软件复杂度
人的大脑本质上是线性的,我们很难处理多线程的东西,也就是一心很难二用。所以降低软件复杂度,本质上就是减少分支。我们经常会谈论架构,其实好的架构就是减少程序的分支,让程序尽可能朝着线性的方向发展。
软件复杂度在软件工程中有一个著名的判定方法McCabe环路。如果一段源码中不包含分支决策点,那么这段代码的圈复杂度为1,因为这段代码中只会有一条路径是线性的,如果这段代码包含了一个分支决策点,那么这段代码圈复杂度为2,以此类推。
McCabe环路有一个很简洁的公式: V(G)=e-n+2。其中e就是下图中变数,n就是节点数。
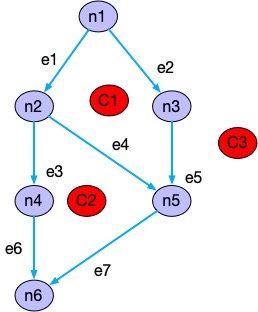
可以计算出上图的软件复杂度为7-6+2=3,从图中可以看出有C1、C2、C3三个区域。下面列出软件复杂度计算的三个方法。
-
流图中的区域数等于环形复杂度。
-
流图G的环形复杂度V(G)=E-N+2,其中,E是流图中边的条数,N是结点数。
-
流图G的环形复杂度V(G)=P+1,其中,P是流图中判定结点的数目。P为出度大于2的。
从上面的公式中,这让我想起来看过的一本书《重构——复杂世界的简单的法则》,所有复杂的东西其实都是由一个最简单的公式,不停的分形迭代造成的。程序的世界尤其适用,所有的复杂性基本都是由if else的分支造成的。所以减少这些环,让我们的程序变的很线性,就是降低软件复杂度的基本原则。
基于上面的简单法则,软件工程发展出来了各种设计模式和架构。这些年流行的函数式编程,其实本质上也是最大限度的让程序阅读起来是线性的,不要出现太多的分支。下面基于日常经常写的代码,展现下如何处理软件的复杂度。
如何降低软件复杂度
下面我用伪代码来演示下,平时经常遇到的一些业务代码问题。业务代码的逻辑很简单就是一位厨师制作食物。
class Cooker {
public Food make {
Food food = new Food();
return food
}
}
class Food {
Food food() {
return self
}
}
void main() {
let cooker = Cooker()
let food = cooker.make()
print("I get {food}")
}
从上面的代码可以清晰的看出,依赖关系很简单Cooker依赖了Food这个对象。这时候产品突然要新增一个需求,说厨师制作的食物完成时,要给厨师的经验提升。如果不假思索,下面的代码实现是最直接的做法。
class Cooker {
int exp
public Food make {
Food food = new Food();
food.handle()
return food
}
public Food addExp {
exp ++
}
}
class Food {
Cooker currentCooker
Food food(Cooker cooker) {
currentCooker = cooker
return self
}
void handle() {
// 制作过程
// ...
// 制作完成
currentCooker.addExp()
}
}
void main() {
let cooker = Cooker()
let food = cooker.make()
print("I get {food}")
}
我们分析下这个需求变更后的复杂度变化。
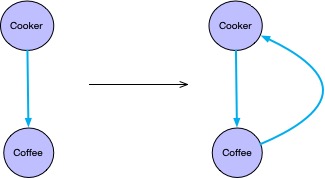
图中可以直观的看出复杂度从1变成了2,其实多思考下这个需求,是否可以降低复杂度那?通过回调或者代理的方式就很容易的降低复杂度,代码如下:
Class Cooker {
int exp
public Coffee make {
let food = new Food();
food.expCallback = () {
exp ++
}
return myCoffee
}
}
Class Food {
void (*ExpCallback)(void) expCallback
Food food(ExpCallback callback) {
return self
}
void handle() {
// 制作过程
// ...
// 制作完成
expCallBack()
}
}
void main() {
let cooker = Cooker()
let food = cooker.make()
print("I get {food}")
}
上面的代码时通过回调的方式解耦,这样Food的类不再依赖Cooker了,就解除了依赖的环,降低了软件的复杂度。如果需要大量的这种回调,其实就可以新建一个类,把回调的方法抽象出来如下.
Class Observer {
void (*CallBack)(void) callback
Observer Observer(CallBack block) {
callback = block
return self
}
public notify() {
callback()
}
}
Class Cooker {
int exp
public Coffee make {
let observer = Observer();
let food = new Food();
observer.callback = () {
exp ++
}
return food
}
}
Class Food {
Observer foodObserver
Food food(Observer observer) {
foodObserver = observer
return self
}
void handle() {
// 制作过程
// ...
// 制作完成
foodObserver.notify()
}
}
void main() {
let cooker = Cooker()
let food = cooker.make()
print("I get {food}")
}
上面的代码就是观察者模式的典型应用场景,其实不同的编程语言可以根据各自的特点实现观察者模式,例如c++常用模板类实现,而Java经常会抽象类来实现。不管如何实现本质上,都是通过抽象出通用的方法,从而使业务的依赖性降低,来减少软件的复杂度。
软件复杂度的原则
从上面的例子中可以看到,当我们在降低软件复杂度的过程中,就诞生了设计模式。下面就再拿设计模式中经典的策略模式举个例子,来说明一下降低软件复杂度常用的一些原则。业务中根据不同的条件执行不同的行为,这种场景再平常不过了。当业务在不停的迭代时,会产生这样的需求例如:”当处理业务A时,需要处理业务B。慢慢的又增加了另一个需求处理业务B时,又要处理业务C。”然后最终的业务代码可能就如下:
Class BusinessA {
handler(int condition) {
if (condition == 1){
let b = BusinessB()
b.handler(1);
} else if(condition == 2){
let c = BusinessC()
c.handler(2);
} else {
let d = BusinessD()
d.handler(condition);
}
}
}
Class BusinessB {
handler(int condition) {
if (condition == 1){
let c = BusinessC()
c.handler(1);
} else {
let d = BusinessD()
d.handler(3);
}
}
}
Class BusinessC {
handler(int condition) {
if (condition == 2){
let b = BusinessB()
b.handler(2);
} else {
let d = BusinessD()
d.handler(3);
}
}
}
Class BusinessD {
handler(int condition) {
print("handler business")
}
}
main() {
BusinessA a = BusinessA()
a.handler(1)
}
上面这种代码就是在若干次业务迭代后,形成了这样的逻辑,我们画下这个业务的流程图如下:
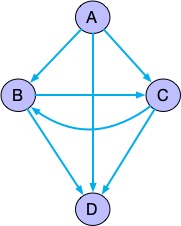
可以看出这种业务的复杂度理解起来非常的困难。下面经过策略模式改造过的代码。
Class BusinessA {
handler(int condition) {
print("handler business A")
}
}
Class BusinessB {
handler(int condition) {
print("handler business B")
}
}
Class BusinessC {
handler(int condition) {
print("handler business C")
}
}
Class BusinessD {
handler(int condition) {
print("handler business D")
}
}
Class Strategy {
handler(int condition) {
switch condition
case 1: {
let a = BusinessA()
let b = BusinessB()
a.hanlder()
b.handler()
}
case 2: {
let a = BusinessA()
let c = BusinessC()
a.hanlder()
c.handler()
}
default: {
let a = BusinessA()
let d = BusinessD()
a.hanlder()
d.handler()
}
print("handler business")
}
}
main() {
Strategy strategy = Strategy(1)
strategy.handler(1)
}
再画出上面代码的业务流程图,可以明显的看出来,采用树形的结构复杂度降低了很多。
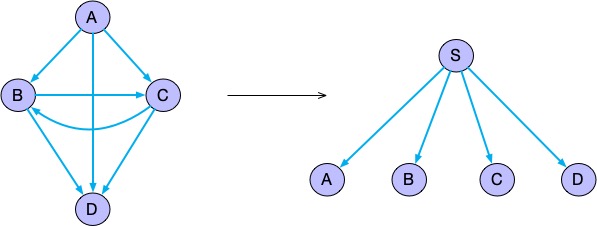
通过上面的这个例子,可以看出减少各个模块的反向依赖,避免反向环的形成,可以有效的降低软件的复杂度。所以我们组织代码结构的时候,尽量组织为树形结构,避免环形成,尤其反向依赖环的形成。反向依赖环不仅使复杂度增加,同时很容易引起潜在的问题,因为环上任意一处有bug影响的是整个环的代码逻辑。而如果是树形结构只会影响当前树的一个分支。
软件架构中,经常提到的高内聚,低耦合,以及设计模式中的接口依赖原则,本质上都是更好的分层。分层的逻辑,简单的来讲就是让程序流程变成一个树形结构,更好的解耦依赖。现在大型的软件基本都是按照树形结构进行设计的,像文件系统,进程管理等等。随着现在软件复杂度的提高,各种框架和架构层出不穷,但本质上万变不离其宗,用上面提到的一个简单公式概况,就是如何让V(G)=E-N+2中的V最小,复杂度降到最低。
总结
有句俗语叫”前人种树后人乘凉”,我们写代码讲武德就是要养成这种美德。每当写下if else或者增加一个全局变量的时候,就得思考下,有没有更好的方法减少这个分支和变量。当我们在设计业务逻辑,一旦出现了环状结构时,就得思考下,是不是分层做的不合理。所以好的代码不仅仅是算法性能一流,也应该是一眼可以看懂的代码,只有这样的代码才能持续的传承下来,才能让后人站在你的肩膀上走的更远。
